No Calculator Is Allowed On This Portion Of The Exam
AP Calculus AB (Section 1, Part A)
Time limit: 0
Exam Summary
0 of 30 Questions completed
Questions:
Information
You have already completed the exam before. Hence you can not start it again.
Exam is loading…
You must sign in or sign up to start the exam.
You must first complete the following:
Results
Exam complete. Results are being recorded.
Results
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
-
You have just completed AP Calculus AB (Section 1, Part A). Take the next portion of the exam by clicking the “Click Here to Continue” button or returning to the AP Calc AB home.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 30
1. Question
Find y’ given that y=3\left(x-4\right)^2-2 .
CorrectIncorrect -
Question 2 of 30
2. Question
Evaluate the Integral I = \int{\frac{18}{t\left(t^6-3\right)}dt} .
CorrectIncorrect -
Question 3 of 30
3. Question
Find the derivative of the function f(t).
f(t) = \frac{t^4+1}{\left(t^4-1\right)^6}
CorrectIncorrect -
Question 4 of 30
4. Question
Use the Trapezoidal Rule to approximate the area under the curve of the differentiable function f\left(x\right) on the interval \left[1,\ 5\right] with n=4,\ as given in the table below:
x 1 2 3 4 5 f(x) 2 6 12 20 30 CorrectIncorrect -
Question 5 of 30
5. Question
If f\left(x\right)=cos\left(x^2-\pi\right) , then f\prime\left(\sqrt{\frac{\pi}{2}}\right) .
CorrectIncorrect -
Question 6 of 30
6. Question
Find the average rate of change of the function f\left(x\right)=x^2+5x from x_1=3 to x_2=8 .
CorrectIncorrect -
Question 7 of 30
7. Question
If \int_{0}^{6}f\left(x\right)dx=10,\ \int_{3}^{0}g\left(x\right)dx=-5 , and \int_{3}^{6}f\left(x\right)dx=6 . Find the value of \int_{0}^{3}\left(2f\left(x\right)+5g\left(x\right)\right)dx .
CorrectIncorrect -
Question 8 of 30
8. Question
Determine the equation of the tangent line to the function x^7+x^5y^4=0 at point (-1, -1) in the form y = mx + b.
CorrectIncorrect -
Question 9 of 30
9. Question
Determine the area enclosed by the curves represented by the provided equations.
y=2x^2-4x+4;\ y=x^2+6x-5
CorrectIncorrect -
Question 10 of 30
10. Question
Evaluate the definite integral: \int_{-\infty}^{0}{\frac{z}{z^4+16}dz} .
CorrectIncorrect -
Question 11 of 30
11. Question
Find the value of \frac{dy}{dx} by differentiating the equation x^4+\frac{1}{7}y^7=6-\frac{5}{3}x^3+y^4 .
CorrectIncorrect -
Question 12 of 30
12. Question
The volume of air in a balloon, V(t), is mentioned by the function V(t) = 100 – 2t² for 0\le t\le5 , where t is the time in seconds. Find the rate, in cubic units per second, at which the volume of the balloon is changing at t = 4 seconds.
CorrectIncorrect -
Question 13 of 30
13. Question
Solve the differential equation.
\frac{dy}{dx}=\frac{y}{x}-cot\frac{y}{x}cos\frac{y}{x} .
CorrectIncorrect -
Question 14 of 30
14. Question
Under optimal laboratory conditions, a bacterial colony experiences exponential growth over time. After 2 hours, the population reaches 8,000 bacteria, and after 4 hours, it increases to 32,000. What was the initial number of bacteria in the colony?
CorrectIncorrect -
Question 15 of 30
15. Question
The graph of function f is shown below:
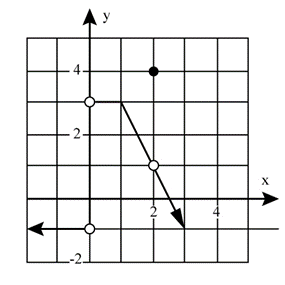
Which of the following statements is false?
CorrectIncorrect -
Question 16 of 30
16. Question
Consider a function f\left(x\right)=x\sqrt{4-x^2} . Find the interval on which the function is concave up.
CorrectIncorrect -
Question 17 of 30
17. Question
If the function f\left(t\right)=-t^3+27t+37 represents the distance of a particle from the origin, at what distance the particle will come to rest.
CorrectIncorrect -
Question 18 of 30
18. Question
Evaluate the integral by using the fundamental theorem of calculus \int_{x-2}^{x}{\frac{t+1}{t}dt} .
CorrectIncorrect -
Question 19 of 30
19. Question
A continuous curve function y=f\left(x\right) is defined such that \lim_{x\rightarrow11}{\frac{f\left(x\right)+23}{x+7}=11} . Find the equation of the line to the curve that is normal to the tangent line at the point \left(x_1,y_1\right) .
CorrectIncorrect -
Question 20 of 30
20. Question
If f(x) = \begin{cases} ax^2 – b & \text{if } x < 1 \\ -1x & \text{if } |x| \geq 1 \end{cases} is differentiable and continuous at x = 1. Find the values of a and b.
CorrectIncorrect -
Question 21 of 30
21. Question
Consider two functions f(x) and g(x), and \left[f\prime\left(4\right)\right]^2-4\left[g^\prime\left(4\right)\right]^2=0 .
Evaluate \lim_{x\rightarrow4}{\frac{f\left(x\right)-f\left(4\right)}{g\left(x\right)-g\left(4\right)}} .
CorrectIncorrect -
Question 22 of 30
22. Question
Find the particular solution of the differential equation log\left(\frac{dy}{dx}\right)=5x+6y at x = 0,y = 0.
CorrectIncorrect -
Question 23 of 30
23. Question
Calculate the volume of the solid of revolution enclosed by the graphs of f\left(x\right)=x^2-6x+3,x=0 , and x = 3 and rotated around the x-axis using slicing method.
CorrectIncorrect -
Question 24 of 30
24. Question
What is the average value of g\left(x\right)=6x^2-2x over the interval \left[-2,3\right] ?
CorrectIncorrect -
Question 25 of 30
25. Question
Is the function given below continuous at x = 2? Why or why not?
f\left(x\right)=7x-2
CorrectIncorrect -
Question 26 of 30
26. Question
Compute the limit and find the horizontal asymptote of the expression:
\lim_{x\rightarrow\infty}{f\left(x\right)=}\lim_{x\rightarrow\infty}\frac{2x^2+3x-5}{4x^3+x^2}
CorrectIncorrect -
Question 27 of 30
27. Question
Let f\left(x\right)=csin\left|x\right|+de^{|x|} is differentiable at x = 0 if
CorrectIncorrect -
Question 28 of 30
28. Question
The function f has a vertical asymptote at x = 8, a horizontal asymptote at y = -11, and f(0) = 0.
What is the possible rational function that meets the given conditions?
CorrectIncorrect -
Question 29 of 30
29. Question
A trough, 12 feet in length, has isosceles triangle-shaped ends with a top width of 4 feet and a height of 1 foot. Water is being poured into the trough at a rate of 9 cubic feet per minute. Determine the rate at which the water level is rising when the water depth is 7 inches.
CorrectIncorrect -
Question 30 of 30
30. Question
Given a continuous function f, the right Riemann sum estimate for the integral \int_{0}^{4}f\left(x\right)dx with n subintervals of equal length is expressed as \frac{4\left(n+2\right)\left(5n+3\right)}{n^2} for all positive integers n. Determine the exact value of the integral \int_{0}^{4}f\left(x\right)dx .
CorrectIncorrect
